Leggyakoribb feladattípusok a központi matematika felvételin

A 8. évfolyamosok számára összeállított felvételi feladatlapon 10 feladat szerepel, melyek megoldására a diákoknak 45 perc áll rendelkezésükre. Nem mellékes információ az sem, hogy mindez a magyar nyelvi feladatlap kitöltése után történik, a kettő közt egy 15 perces szünettel,

 így a stresszkezelés mellett, a hosszan tartó koncentrálóképességet sem árt fejleszteni.

 

„A matematika feladatlapok nem kizárólag a tantárgyban tanultakat mérik, hanem ehhez kapcsolódóan a tanulók gondolkodásának jellemzőit is. Az ismeretek alapeszközként szolgálnak a feladatok megértéséhez, a problémák megoldásához. Bizonyos feladatok megoldásának folyamatában a vizsgázónak többféle kompetenciát is mozgósítania kell. A feladatmegoldás sikerességében a tantárgyi ismeretek mellett fontos szerepet kaphat a feladatmegoldó készség, a problémaérzékenység, a kreativitás, a logikai biztonság, a szabálykövetés, a koncentráló képesség, vagyis a figyelem összpontosítása és tartóssága. Fontos kompetencia az életkori sajátosságoknak megfelelő szintű írásbeli kommunikáció is. Ebből következően elvárás a megoldások rendezett, olvasható, követhető írásos rögzítése.”
Oktatási Hivatal

Nézzük meg, hogy

melyek a leggyakrabban előforduló feladattípusok matematikából!

 

A Webkurzus felvételi előkészítő témaköreinek összeállításához végignéztük az Oktatási Hivatal honlapján elérhető, 2004 óta kiadott feladatlapban előforduló feladattípusokat.

A lenti grafikonon látható, hogy melyik feladattípus hányszor fordult elő ez idő alatt.

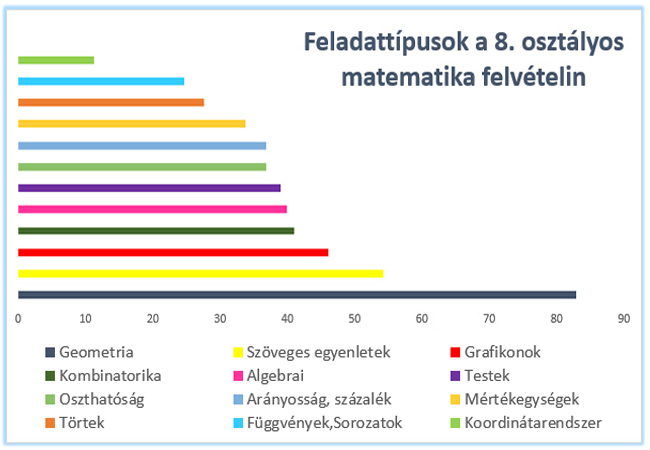
Természetesen vannak olyan feladatok, melyek több típusba is sorolhatók, hisz a matematika szépsége ebben rejlik. Például egy grafikon elemzésénél rákérdezhetnek az adatok százalékos összefüggéseire is, vagy egy geometriai feladat tartalmazhat mértékegység átváltást is.

A matek központi felvételi feladatlapoknál az utóbbi időben beállt egy rend,
mely természetesen bármikor megváltozhat,
de az elmúlt években az alábbi szerkezet ismétlődik:

 

Az első feladat valamilyen algebrai műveletre kérdez rá, a legtöbb esetben a törtekkel való műveleteket kell itt nagyon jól tudni.

Ezután a mértékegységátváltással kell megküzdeni, de az algebrai műveleteket ide is becsempészték.

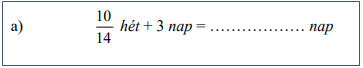
A harmadik feladat a kombinatorika, azaz egy szöveg alapján el kell dönteni, hány, a feltételeknek megfelelő megoldás létezik az adott problémára. Itt nagyon fontos a szövegértés, és hogy a gondolatait egy logikai szálon tudja végigfuttatni a diák, ugyanis az esetek többségében, nem tudni előre, hány megoldást kell megtalálnia.

Található még a feladatok között grafikon elemzése, ahol az egyik kérdés megválaszolásához nem árt, ha tud a diák százalékot számítani.

Az ötödik feladat geometriai ismereteket kíván, általában szögeket kell kiszámolni egy megadott alakzatban, így nem árt tudni a szögek közötti összefüggéseket sem.

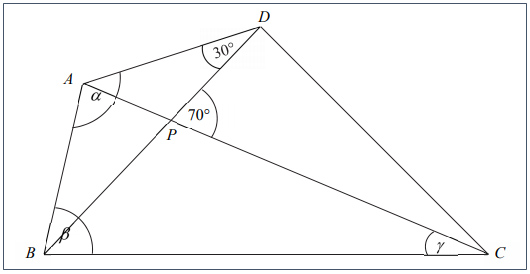
És itt kezdődik a neheze, jönnek a szöveges feladatok…

 

Ezeket nagy fantáziával rendelkező tanárok állítják össze, így minden évben tudnak valami újat kérdezni. Itt derül ki, hogy ki az, aki a tantárgyi ismeretek mellett jó feladatmegoldó készséggel, problémaérzékenységgel, kreativitással van megáldva. Itt érik össze a matematikai készség a másik gyenge ponttal, a szövegértéssel.

Az azért elmondható, hogy az egyik feladat általában arányosság felismerését kívánja meg,

a másik pedig jó modellalkotási készséget kíván:

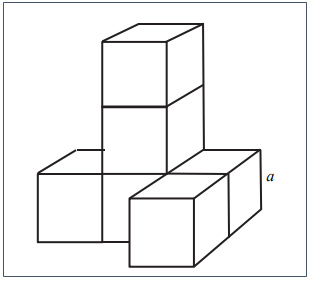
Szerepel a feladatok között térgeometriai, azaz egy testnek kell kiszámolni a felszínét, térfogatát, illetve meghatározni az éleinek, csúcsainak, lapjainak számát.

Ehhez elengedhetetlen a jó térlátás, és a felszín és térfogat fogalmának ismerete.

Az utóbbi pár évben bekerültek teszt típusú feladatok is, ahol „csak ” ki kell választani a helyes megoldást. Itt bármi előjöhet, gyakoriak az oszthatósággal kapcsolatos kérdések.

Ehhez hasonló, amikor állításokról el kell dönteni, hogy igazak vagy hamisak. Rosszabb esetben, hogy lehetségesek, lehetetlenek vagy biztosak. Itt is geometriai és oszthatósággal kapcsolatos kérdésekre számíthat a felvételiző diák.

Fontos tudni, hogy a 2024-es felvételi feladatok követelményei már a NAT2020-hoz lesznek igazítva. Így függvényekre nem kell számítani, azonban bekerülhetnek feladatok a számrendszerek témakörből.

A fentiek alapján levonható következtetések után a Webkurzus matematika előkészítője az alábbi témaköröket dolgozza fel részletesen:

1. Algebra
2. Törtek
3. Grafikonok, egyszerű statisztikai számítások
4. Mértékegységek
5. Oszthatóság
6. Arányosság
7. Kombinatorika
8. Geometria
9. Koordinátarendszer, Geometriai transzformációk
10. Egyenletek
11. Testek
12. Sorozatok/Halamzok

Ha pedig az aktuális matek felvételis trendek mellett
a tavalyi feladatok pontos tartalmára és megoldására vagy kíváncsi…

 

a tavalyi évhez hasonlóan idén is megnézhetitek a helyes megoldásokat rövid magyarázatokkal ellátott videókon – a feladatok között a videó alján lévő lapozógombbal tudtok navigálni!